STEM and ELT: Math Modeling Builds Vocabulary, Too!

When people first think of math modeling, the usually think of either bar modeling or Singapore Math Model Drawing, because it is one and the same. It is a method of visualizing math word problems and also a method of expanding on the word problem as well. What many people don’t consider is that it can be used to build and visualize vocabulary, too: the number one obstacle for many multilingual learners of English (MLEs). It is researched that a person needs to know 90% of the vocabulary in a text for minimal reading comprehension and 95% for adequate comprehension.

According to Bernado, MLEs who have had formal education in their home countries generally do not have mathematical difficulties; hence, their struggles begin when they encounter word problems in an additional language that they have not yet mastered. For this reason, it is recommended that students learn key terminology prior to attempting to solve mathematical word problems. One way to do this aside from using the Frayer Model or having students write definitions is to “model” the vocabulary as much as possible.  Let’s look at an example from Bill Davidson’s Problem Solving Ladders to model “less than” and “more than,” which are quantitative relationships that are known to cause MLEs difficulties when solving word problems.

Example 1

You will notice that there is not a question for this problem. This is a powerful strategy because it allows you to focus on the vocabulary portion of your lesson; otherwise, students in your class who know the math and the English will immediately jump to solving the problem instead of listening to your lesson on vocabulary. You then create the bar model of the problem, which will lend itself to the vocabulary lesson:

Teacher: [reading the word problem] Tarrence has 27 dollars and 68 cents. Saimeen has 17 dollars and 85 cents, and Lena has three dollars and ten cents. Who has the largest amount of money?

Class: Tarrence.

Teacher: Correct.  So, Tarrence’s bar must be the longest. Who has the next largest amount of money, between Saimeen and Lena?”

Class: Saimeen. He has 17 dollars and 85 cents.

Teacher: Correct. So I have to draw Saimeen’s bar shorter than Tarrence’s bar. Since Lena has the smallest amount of money. Her bar has to be smaller than both Tarrence and Saimeen.  Notice that the length of the bars reflect the amount of money. Since 27 dollars and 68 cents is not a whole lot more than 17 dollars and 85 cents, the bar’s length will not be very different in size. But, since Lena’s amount of 3 dollars and 10 cents is much smaller than Saimeen’s and Tarrence’s, Lena’s bar must be much smaller than the bar lengths of Tarrence and Saimeen.

Next, the arrows are drawn to show the difference in arrow length between Tarrence, Saimeen, and Lena.

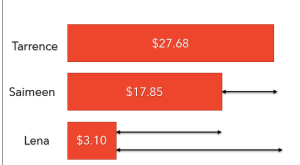
The arrows will help in explaining “more than” and “less than.”

Teacher:  Tarrence has more money than Saimeen and Lena. We can tell this by the length of Tarrence’s bar, which is longer than both Saimeen and Lena’s bar. To be more specific, we can say that Tarrence has $9.83 cents more money than Saimeen. We can also say that Saimeen has $9.83 less than Tarrence, and that Lena has $24.58 less than Tarrence.

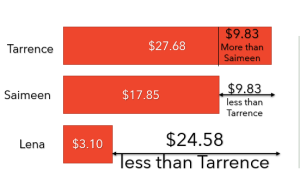
The same comparisons can be made between Lena and Saimeen using the difference in money in the bar model.

Example 2

135 girls entered a school art competition. Fifteen fewer boys than girls entered the competition. How many boys entered the competition? How many more girls than boys were at the competition?

Remember: remove the question so that the students will focus on your lesson for the vocabulary.

135 girls entered a school art competition.  Fifteen fewer boys than girls entered the competition. 

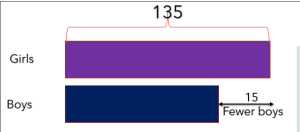
Teacher: Are there more girls or boys at the art competition?

Class: Girls.

Teacher: How do you know?

Class: The bar for girls is longer than the bar for the boys.

Teacher: Correct. So we can say that there are fewer boys than girls, which means that the number of boys is smaller or less than the number of girls.

Now the teacher can include the question and have the students solve the word problem: How many boys entered the competition? How many more girls than boys were at the competition?  

Teacher: So, to figure out the answer, what is the math operation that is needed? Addition, subtraction, multiplication, or division?

Class: Subtraction, because the bar for the boys and the difference of 15 boys must equal the length of the bar for the girls.

This is just one way to use bar  modeling to teach vocabulary visually. Next month, we will discuss how bar modeling is also very effective in solving multistep word problems, which can cause a lot of confusion with your MLEs. These problems are often based on language such as “of the remaining,” “twice as many,” and “half of the remaining,” which is challenging for MLEs because it has to deal with the relationships between two or more words.

Do you have any strategies to share that you use to visually teach vocabulary? Please share with us in the comments section below.